Fashion & Mathematics: Is there a connection we rarely see?

When seeing or hearing the words Fashion and Mathematics, would you think they’re related? Could you ever imagine saying that you’re studying mathematics to become a fashion designer? Most probably not, but maybe this idea is not as far-fetched as you may think. Many people see the worlds of fashion and mathematics as two completely different domains but what if I told you that these two fields interact more often than we think and that they complement each other. Do you think math was used to make the very clothes you’re wearing now? Think about it. Picture this: using math to create and produce clothing but also to explore different types of fashion prints and designs or maybe even using art, more specifically fashion to unravel math concepts.

This is already done today! Fashion through clothing production in itself has math incorporated in their day-to-day tasks. When starting the process of making clothes, designers usually start with a sketch. This sketch can be made freehand or by using computers, or both.

(Fashion & Geometry Comparison, 2013)

In the sketches designers are essentially drawing shapes, lines, constructing angles, and ensuring symmetry or the intentional lack thereof, which is all part of geometry. Geometry being a fundamental branch of mathematics is the study of shapes, patterns, sizes, and their relation to each other in space.

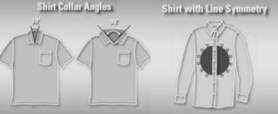
(Bertoletti, 2009)

Nanneke Linders, freelance fashion and print designer based in Utrecht, mentioned that textile design within fashion has lots of math incorporated into it. By definition, a textile is a flexible material made by creating interlocking bundles of yarn or thread. Textiles are then formed by weaving, knitting, crocheting, knotting, felting, bonding, or braiding yarn together. Textiles do not necessarily have to be used in the production of clothing. However, when textile production is used to make a fabric, these textiles can be used to produce clothing. It just requires one additional step: the clothing construction.

Abstract Textile Example

Many may wonder how textile design uses mathematics and why it is mathematical. In textile design, geometry is used to define how the design elements are laid out and how they relate to each other. Geometry helps to define the structure of how elements are placed in a design. An example of this is how vertical and horizontal lines are arranged within striped or checkered clothing.

Nanneke stated, “Half drop designs, and building a pattern can be very mathematical”. Tafari Lake, fashion student at Amsterdam Fashion Academy, also agreed that to create a pattern, basic mathematical skills were needed. This is because geometry is involved in constructing pattern repeats, which is how a segment within a design replicate throughout a fabric surface, allowing textiles to have smooth endless repeating patterns without any borders or boundaries. For example, not having a line or gap between a print. Tessellations are an example of this. Pattern repeats are based on different variations of vertical and horizontal lines on a geometric grid. The “full drop” is where a design element repeats in a straightforward grid (e.g., basic checkered prints) and the “half drop” where the design element is staggered in rows. This half drop and full drop is all about how designers shift elements around on a geometric grid.

Even within very abstract designs, there may be the inclusion of triangles, squares, circles, zigzags, differing in the extent which geometric elements are used. Organic patterns on the other hand are patterns comparable to elements found in nature, they can be either geometric or not depending on the chosen pattern, as there is geometry within nature.

(Fisher, 2007)

The most common example is observed in fractals. A fractal is a pattern where the laws of nature repeat at different scales and examples are tree branching or snowflakes. Thus, designers tend to combine abstract and organic designs to come up with new patterns. Therefore, using the geometry within nature-based and abstract patterns, to create new designs.

This is however more about how mathematics works as an underlying tool for designers to create prints. On the more contemporary side, ever heard of Mame Diarra Bousso Gueye? She is a fashion designer from Senegal but is also a mathematician. Through her fashion brand called DiarraBlu, she fuses her passion for mathematics and Senegalese culture into her clothing.

(Jallow, 2020)

(The Math Lab with DIARRABLU: Fashion Incubator San Francisco, 2019)

She produces fashion inspired by mathematics as she uses mathematical equations; namely exponential and quadratic functions to create new fashion prints and patterns.

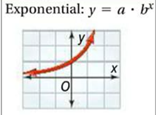
Exponential Graph

An exponential function is a function whose value is a positive constant other than 1 that is raised to a variable exponent, and even more so when the constant within the function is the value e. The function is generally denoted by f(a)=b•cª or f(a)=eª . Exponential functions increase, hence rise or fall and  decrease quickly in one direction.

Quadratic functions are polynomials of degree 2, meaning the variable within the function cannot be raised to a power higher than 2. A quadratic function is given in the form f(x)=ax²+bx+c where a, b, and c are numbers that are equal to zero.

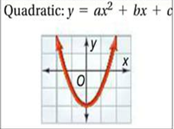
Quadratic Graph

When graphing quadratic functions, a “U” shape is formed, either upwards or downwards, varying in width or steepness. This U-shape formed by a quadratic function is called a parabola in mathematics.

Could you imagine seeing mathematical equations graphed and thinking what a lovely fashion print this would make? Most of us won’t. When speaking to both Nanneke and Tafari, they both implied that once someone has a background or more naturally thinks of math to solve things, it becomes easier to implement math within their fashion. Tafari stated “Those who have a passion for math will always find a way to incorporate more math into their designs. In my opinion, the use of mathematical algorithms is only necessary for mass production of clothing as it’s probably more time efficient, but for now I prefer sketching freehand is sufficient for me.” Additionally, Nanneke mentioned “My husband is also a textile designer, and he has (just from who he is) a more mathematical approach, as he has a better understanding of math”.

Miss Bousso is also a secondary mathematics teacher in California and has been a Mathematics Specialist at the International School of Dakar (ISD). She generally has a creative approach towards mathematics and uses this approach to show students that math is more than a bunch of abstract concepts, by joining it with art, in this case fashion. Her goal is to get more African students, specifically females interested and engaged in Mathematics and other STEM fields. It has been conveyed that her female students become more excited about STEM when fashion is involved, the involvement makes them feel like they belong in math class, which may further translate to math occupations. Scientific research also suggests that integrating STEM into the study of fashion design can improve students’ creative and academic performance. This supports the idea of fashion being used as an instrument to unravel and further explore mathematical concepts.

Through people’s love for nice patterns in clothing and always being on the lookout for new styles and patterns, who knows, there may be more mathematical influence in fashion design in the years to come. As we have seen that new patterns can come to life with the use of geometry. In the future, we may also have a field dedicated to mathematical fashion designers. Further seeing the beauty and versatility of mathematics and bridging the perceived disconnect between math and fashion, as one can indeed use math to create and explore different fashion print designs and fashion can be used to explain and deduce math concepts.

Now I guess you may think differently of the clothes you’re wearing right now; do you recognize some math/geometry?

References

Bertoletti, J. C. (2009). How Fashion Designers Use Math (Math in the Real World). Chelsea Clubhouse.

Fisher, G. (2007). High Fashion Goes Mathematical. Math Horizons, 15(1), 22–24. https://doi.org/10.1080/10724117.2007.11974725

Jallow, R. (2020, November 22). DiarraBlu – Where Math Meets Fashion. Djellibah. https://djellibah.com/en/home/2020/11/20/diarrablu

The Math Lab with DIARRABLU — Fashion Incubator San Francisco — Supporting Designers in the Business of Fashion. (2019, December 14). FiSF. https://fashionincubatorsf.org/events-1/the-math-lab-with-diarrablu

Philipkoski, K. (2021, November 1). How Fashion Saved This High School Math Teacher’s Life. Forbes. https://www.forbes.com/sites/kristenphilipkoski/2019/12/23/how-fashion-saved-this-high-school-math-teachers-life/?sh=25752c1d5a25

Quick Fashion and Geometry Comparison (With Some Architecture and Set Design Thrown in). (2013, July 26). Irenebrination: Notes on Architecture, Art, Fashion, Fashion Law & Technology. https://irenebrination.typepad.com/irenebrination_notes_on_a/2013/09/lina-bo-bardi-preen-spring-2014.html

Ye, J. H., Hong, J. C., & Fan, J. Y. (2019). STEM in Fashion Design: The Roles of Creative Self-Efficacy and Epistemic Curiosity in Creative Performance. EURASIA Journal of Mathematics, Science and Technology Education, 15(9). https://doi.org/10.29333/ejmste/108455

Interview held with Fashion Designer, Nanneke Linders (02/11/2021)

Interview held with Fashion Student, Tafari Lake (03/11/2021)